Sunday, August 13, 2006
Hatching a thicker plot
Forrest has been working on bitmap-based infill algorithms for depositing the build material in layers; these have the advantage of being very robust, but they are a bit memory hungry.
Meanwhile, I have been improving the infill routines for the Java CSG representation.
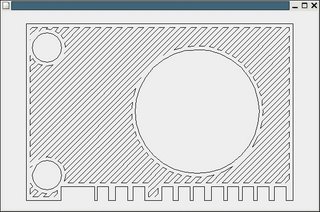
Above is a test piece. The outer rectangle and the circles are the delineation of the shape that the machine lays down first. It then follows the hatch lines to infill between those boundaries. The hatch needs to be offset by the stream width inside the boundary (and the outer boundary needs to be offset inwards by half that width from the true boundary). The hatch follows a series of "pen down" movements that are all connected to minimise the amount of "pen up" movement.
Well. I say minimise. It's actually a fast heuristic. A true minimisation would be a travelling-salesman solution, which would probably be a bit slower...
Meanwhile, I have been improving the infill routines for the Java CSG representation.

Above is a test piece. The outer rectangle and the circles are the delineation of the shape that the machine lays down first. It then follows the hatch lines to infill between those boundaries. The hatch needs to be offset by the stream width inside the boundary (and the outer boundary needs to be offset inwards by half that width from the true boundary). The hatch follows a series of "pen down" movements that are all connected to minimise the amount of "pen up" movement.
Well. I say minimise. It's actually a fast heuristic. A true minimisation would be a travelling-salesman solution, which would probably be a bit slower...
Comments:
<< Home
Just thought I'd note that the traveling salesman problem in the euclidean plane is solvable in polynomial time, and I think not terribly large polynomial time. You get to assume things like the shortest distance between two nodes is the edge between them... it stops being NP-complete the moment you can make that assertion. Of course, the heuristic may very well be faster and certainly will do the job just fine.
Adrian, how long do you reckon until this is in the subversion repository? I should have the Mk 2a extruder fired up and callibrated in a couple of days. Then I can try and make a real honest-to-goodness part :)
Vik :v)
Vik :v)
Vik - I've just removed some of the debugging reporting and checked it all back in. Should be ready to go.
Is there a reason for using diagonal infill instead of using lines parallel to one of the sides?
***
Just thought I'd note that the traveling salesman problem in the euclidean plane is solvable in polynomial time,
***
I believe euclidean travelling salesman problem is still NP-Hard, but has been shown to be subexponential in time complexity (still larger than polynomial.)
There are polynomial time algorithms with solutions within a factor of the optimal solution.
***
Just thought I'd note that the traveling salesman problem in the euclidean plane is solvable in polynomial time,
***
I believe euclidean travelling salesman problem is still NP-Hard, but has been shown to be subexponential in time complexity (still larger than polynomial.)
There are polynomial time algorithms with solutions within a factor of the optimal solution.
I just do a bit of a search for things that are near to each other...
Hatch angle - this can be at any angle (including 0 and 90). 45 degrees and -45 degrees on alternating layers give good ply strength, but you could have lots of strategies: clock round by +30 from one layer to the next, for example.
Also you can do all sorts of tricks (I haven't, yet) with gaps to give sparse infill and so on. In particular you can do the outline, offset to do a dense fill in to (say) 3 mm shell thicness, then sparse fill the void in the middle of that. It's quite easy to do the vertical calculations needed to get (near) horizontal planes to have the same shell thickness.
Hatch angle - this can be at any angle (including 0 and 90). 45 degrees and -45 degrees on alternating layers give good ply strength, but you could have lots of strategies: clock round by +30 from one layer to the next, for example.
Also you can do all sorts of tricks (I haven't, yet) with gaps to give sparse infill and so on. In particular you can do the outline, offset to do a dense fill in to (say) 3 mm shell thicness, then sparse fill the void in the middle of that. It's quite easy to do the vertical calculations needed to get (near) horizontal planes to have the same shell thickness.
*** (and the outer boundary needs to be offset inwards by half that width from the true boundary). ***
This was the problem I was trying to solve on the reprappers page. How do you do this currently, and does it deal with the problems I noted in my own investigations? When I looked at the java code, it appeared that you were simply doing half-plane intersections after offsetting by half the thread width -- this has the problems I noted when you try to trace fairly acute inner angles (Maybe these aren't going to happen much for actual models?)
Also, is/should there there be concern about the possibility that the Z thickness in the thread would alter the tolerances you'd have along the Z axis, for planes that were not parallel with the working surface?
This was the problem I was trying to solve on the reprappers page. How do you do this currently, and does it deal with the problems I noted in my own investigations? When I looked at the java code, it appeared that you were simply doing half-plane intersections after offsetting by half the thread width -- this has the problems I noted when you try to trace fairly acute inner angles (Maybe these aren't going to happen much for actual models?)
Also, is/should there there be concern about the possibility that the Z thickness in the thread would alter the tolerances you'd have along the Z axis, for planes that were not parallel with the working surface?
***
... then sparse fill the void in the middle of that.
***
Sounds like a good idea. Would there be any possibility of using two heads? A fine head (.5mm or smaller) and a course head (2mm+), and use the course thread for the inner core (Printing 20 threads at 2mm covers the same volume as 320 threads at .5mm for the same length)
... then sparse fill the void in the middle of that.
***
Sounds like a good idea. Would there be any possibility of using two heads? A fine head (.5mm or smaller) and a course head (2mm+), and use the course thread for the inner core (Printing 20 threads at 2mm covers the same volume as 320 threads at .5mm for the same length)
beaglefury: you are, of course, correct. I was misremembering the result for a constant factor approximation as a precise solution, and the mechanism for deriving a precise solution to some NP-complete problem or other from a constant-bound approximation of the general TSP. Constant-factor approximations of the general TSP are NP-hard, and constant-factor approximations of the TSP with the triangle inequality to within 1.5 are not.
I feel silly now.
That said: subexponential? that would be a fairly impressive result - I'd like to see where that was determined, as that would show that every problem in the class NP can be solved in less than exponential time, which I'd not heard about.
I feel silly now.
That said: subexponential? that would be a fairly impressive result - I'd like to see where that was determined, as that would show that every problem in the class NP can be solved in less than exponential time, which I'd not heard about.
Offsetting: The object is represented as both unions and intersections of half-planes. I _think_ that if you keep the boolean combination of these the same and just move them all by the offset distance you always get the right answer. But maybe BeagleFury has a counterexample. Can you draw it?
Two heads - the ultimate RepRap design will have a whole row of heads and go and pick up whichever is needed next...
Two heads - the ultimate RepRap design will have a whole row of heads and go and pick up whichever is needed next...
*** But maybe BeagleFury has a counterexample. Can you draw it? ***
Sorry - you have on the reprappers blog. Can't check everything at once!
Yes - that problem goes away completely with a CSG representation. The offset shape eventually falls (correctly) into two disjoint shapes.
Sorry - you have on the reprappers blog. Can't check everything at once!
Yes - that problem goes away completely with a CSG representation. The offset shape eventually falls (correctly) into two disjoint shapes.
Yes. The example on the reprappers blog illustrates the issue with acute inner angles. Without clipping the inner angles, you introduce seams / weak point into models that otherwise could have been printed without the weaker joint (if you clip the interior angles.)
The perfect curve, if it could be found, is the set of all points C such that C an element of the polygon, and |X-C| = d for any point X not in the polygon, where d is 1/2 the thread width and |P| is the length of vector P. Your solution is correct everywhere except for acute angles. I wonder if one could add some circles with diameter d at acute inner angle vertices, and figure out the appropriate boolean intersection with the lines to add in the acute angle clipping without the fancy stuff I did with vector algebra. I'll think about it a little.
This would be a pretty good solution, because the reprap hardware should be able to print lines and partial-circles using only integer addition and comparison.
The perfect curve, if it could be found, is the set of all points C such that C an element of the polygon, and |X-C| = d for any point X not in the polygon, where d is 1/2 the thread width and |P| is the length of vector P. Your solution is correct everywhere except for acute angles. I wonder if one could add some circles with diameter d at acute inner angle vertices, and figure out the appropriate boolean intersection with the lines to add in the acute angle clipping without the fancy stuff I did with vector algebra. I'll think about it a little.
This would be a pretty good solution, because the reprap hardware should be able to print lines and partial-circles using only integer addition and comparison.
Ah! What you want is GLADES (graphical lamina designer), by John Woodwark (see MEG on the reprappers blog).
This represents a shape as an ordered list of circles with signed radii. You visit each circle tangentially, the tangent choice out of the two possibilities being made by the radius sign (which essentailly tells you to arrive and leave clockwise or anticlockwise). A radius of 0 gives a sharp corner.
To offset this by D just add or subtract D to/from all the radii, and everything comes out in the wash...
This represents a shape as an ordered list of circles with signed radii. You visit each circle tangentially, the tangent choice out of the two possibilities being made by the radius sign (which essentailly tells you to arrive and leave clockwise or anticlockwise). A radius of 0 gives a sharp corner.
To offset this by D just add or subtract D to/from all the radii, and everything comes out in the wash...
Yeah, I was considering representing the extruder path using a data structure of 5 variables to describe any directed line segment or directed circular arc.
The CSG algorithm could probably be adapted to include these arc regions, but unless you wanted to include spheres and circles as primitive shapes, I'm not sure it's worth it. A line approximation for the circle in the offset polygons at the points where it actually count has pretty low error (in terms of area).
There is still situations where thread could overlap voids above and/or below the current extrusion plane -- I think it's more an intellectual problem than a practical one though.
Post a Comment
The CSG algorithm could probably be adapted to include these arc regions, but unless you wanted to include spheres and circles as primitive shapes, I'm not sure it's worth it. A line approximation for the circle in the offset polygons at the points where it actually count has pretty low error (in terms of area).
There is still situations where thread could overlap voids above and/or below the current extrusion plane -- I think it's more an intellectual problem than a practical one though.
<< Home
